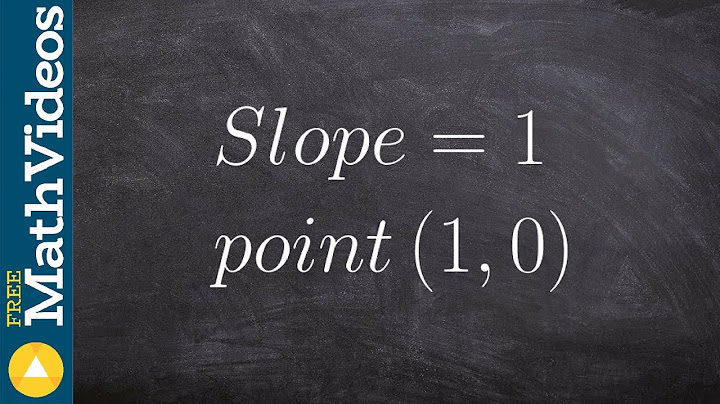How do i find the center of a circle

Whether you’re drilling holes in a flower pot or dabbling in carpentry, finding the exact center of a circle can be a challenge. Here’s an easy solution for finding the center of a circle that will work with any project or material.

How to Find the Center

Remember high-school geometry? Yeah, me neither. But whether you know it or not, you’ll be using geometry for this simple task, specifically Thales’ Theorem and the idea that right angles always cut a circle through its diameter.

To find the center of a circle, all you need is a 90-degree angle and a straight edge. A framer’s square has both, but you can improvise with a piece of cardboard, paper, or whatever you have on hand, as long as the corners are 90 degrees.

Step 1

Lay the square on top of the circle, with the right angle touching the edge. Don’t worry about positioning – the beauty of the theory is that it doesn’t matter.

Step 2

Mark the circle where the sides of the square cross the edge of the circle.

Step 3

Using a straight edge (one side of the square works great), draw a line connecting the two marks.

Step 4

Reposition the square so the right angle touches the edge in another spot, and repeat steps 1-3.

Step 5

Now you have an “X” marking the center of your circle. Pretty easy, huh?

Step-by-step examples of finding the center and radius of circles

Example

Find the center and radius of the circle.

???x^2+y^2+24x+10y+160=0???

In order to find the center and radius, we need to change the equation of the circle into standard form, ???(x-h)^2+(y-k)^2=r^2???, where ???h??? and ???k??? are the coordinates of the center and ???r??? is the radius.

In order to get the equation into standard form, we have to complete the square with respect to both variables.

Grouping ???x???’s and ???y???’s together and moving the constant to the right side, we get

???(x^2+24x)+(y^2+10y)=-160???

Completing the square requires us to take the coefficient on the first degree terms, divide them by ???2???, and then square the result before adding the result back to both sides.

The coefficient on the ???x??? term is ???24???, so

???\frac{24}{2}=12???

???12^2=144???

The coefficient on the ???y??? term is ???10???, so

???\frac{10}{2}=5???

???5^2=25???

Therefore, we add ???144??? inside the parentheses with the ???x??? terms, ???25??? inside the parenthesis with the ???y??? terms, and we also add ???144??? and ???25??? to the right with the ???-160???.

???(x^2+24x +144)+(y^2+10y+25)=-160 + 144+25???

Factor the parentheses and simplify the right side.

???(x+12)^2+(y+5)^2=9???

Therefore, the center of the circle is at ???(h,k)=(-12,-5)??? and its radius is ???r=\sqrt{9}=3???.

Example

What is the center and radius of the circle?

???6x^2+6y^2+12x-13=0???

In order to find the center and radius, we need to change the equation of the circle into standard form, ???(x-h)^2+(y-k)^2=r^2???, where ???h??? and ???k??? are the coordinates of the center and ???r??? is the radius.

In order to get the equation into standard form, we have to complete the square with respect to ???x???. The ???y??? term is already a perfect square.

Let’s begin by collecting like terms and moving the ???-13??? to the right.

???6x^2+12x+6y^2=13???

Our next step is to remove the coefficients of the second degree terms of the ???x??? variable and ???y??? variable. First, we’ll factor out a ???6??? then divide by ???6??? on both sides.

???6(x^2+2x+y^2)=13???

???x^2+2x+y^2=\frac{13}{6}???

Now complete the square of the ???x??? terms. The ???y??? term is already a perfect square.

???(x^2+2x)+y^2=\frac{13}{6}???

Completing the square requires us to take the coefficient on the first degree term, divide it by ???2???, then square the result before adding the result back to both sides. 

The coefficient on ???x??? is ???2???, so

???\frac{2}{2}=1???

???1^2=1???

We’ll therefore add ???1??? to both sides, and get

???(x^2+2x+1)+y^2=\frac{13}{6}+1???

Factor the ???x??? terms and simplify the right hand side.

???(x+1)^2+y^2=\frac{19}{6}???

If you want, you may also write the equation as

???(x+1)^2+(y+0)^2=\frac{19}{6}???

The center of the circle ???(h,k)??? is ???(-1,0)??? and the radius is ???\sqrt{19/6}???. Rule out ???-\sqrt{19/6}??? because a radius can't be negative.

Get access to the complete Algebra 2 course

How do you find the center of a circle to drill a hole?